名前なし
2025/09/13 (土) 19:09:49
290f1@1fcc6
ちょっと検算お願いできませんか?
Lv.50目前の子のサブスキルが下から順に
おてつだいスピードS、最大所持数アップS、食材確率アップSです。
おてスピと食確のどっちもがMになったら終了の銀たねチャレンジする場合、
今とLv.50後の2回に分けてチャレンジするのと
Lv.50になってから一度にチャレンジするのとでは、
必要な銀たね枚数って期待値3.333…で同じですよねえ?
通報 ...

IQ5000の私がお答えしよう
当たるか当たらないかなので二分の一ですね
いや、レベル50になってから抽選した方が必要な銀種の数は減りますよ
レベル50未満からだと13/4で、レベル50からだと55/18かな?
シンプルに考えて「1/2に2回勝つ」のと「2/3と1/2に勝つ」だったら後者の方が勝率高い
あれ、なんでだろ?
Lv.50前でのチャレンジはLv.10に当たるまで続けるから1、2、3個の3通り。
1個で済んだ場合はLv.50になってからLv.50に当たるまでさらに1、2、3個の3通り。
2個で済んだ場合はさらに1、2個の2通り。
はじめに3個使っちゃった場合は追加で1個の1通りだけ。
トータルでは6通りで、それぞれで使う個数の合計は20だから20/6で3.33…個と思ったんです。
Lv.50過ぎてからまとめてチャレンジしても、10と50の順が逆になったパターンが入るだけなので
40/12=3.333…個で同じなのかなあ、と。
どこがおかしいんだろ?
期待値 = 使う個数×その個数になる確率 の合計
なので、個数を場合数で割ることができるのは、確率がすべて同じときのみです
それぞれの確率
p1-1:手|食 = 1/2 × 1/2 = 1/4
p1-2:手|所食 = 1/2 × 1/2 × 1/2 = 1/8
p1-3:手|所所食 = 1/2 × 1/2 × 1/2 * 1 = 1/8
p2-1:所手|食 = 1/2 × 1/2 × 1/2 = 1/8
p2-2:所手|所食 = 1/2 × 1/2 × 1/2 × 1 = 1/8
p3-1:所所手|食 = 1/2 × 1/2 × 1 × 1 = 1/4
期待値 = 2×1/4 + 3×(1/8 + 1/8) + 4×(1/8+1/8+1/4) = 13/4
木主じゃないけど紙に書いて考えてたんだけど
まとめてのほう
②コ 12/36
③コ 10/36
④コ 14/36
こうなったんだけど
ここから期待値を出すって
2×(12÷36)=0.666...
3×(10÷36)=0.833...
4×(14÷36)=1.555...
こうなってこれらを足すと
3と1/18 になるらしい
分割が13/4(3と1/4)になるなら
まとめてのほうが数が小さい・お得!
これであってる?
両方とも計算しましたが>> 1527さんと同じ結果になりました
>> 1534それはシンプルに「2回連続で勝つこと」しか考えていない計算では?
>> 1538「1、2、3個の3通り」これは同じ確率ではないですね
所持数に当たる確率から考えるとして、
①Lv.50になる前の場合 → おてスピに当たる確率は1/2、所持数に当たる確率は1/2
②Lv.50になった後の場合 → おてスピ+食確に当たる確率は2/3、所持数に当たる確率は1/3
②で仮におてスピに当たった場合、食確に当たる確率は1/2、所持数に当たる確率は1/2
つまり、Lv.50を超えてから銀種を使用したほうが所持数に当たる確率を下げられるので、銀種の使用個数の期待値も下がるという認識だけど合ってるかな。
わー、みなさんありがとう。
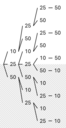
暗算で分数のたし算かけ算するのあきらめて期待値はハッキリ言うとどうでもいいと思ってました。
ちゃんと計算してくださった方たちありがとです、ごめんなさい~。
言いたかったのは、直感的には、2段階抽選なら確率が同じ分岐が対称に半分消えるだけだからいっしょやん、
って思ったってことなんですよね。
(直感部分を説明するには文字じゃ難しくて図にするしかなかった😅)
その図ベースで直感的にいうなら中央が半分になってるのを埋めた分だけ外れやすくなってるって感じかな